ТЕМА 4.8. Движение воды в пористой среде
• Движение грунтовых вод является частным случаем фильтрации – движения жидкости в пористой среде.
• Фильтрация происходит через поры грунта и может быть ограничена снизу и сверху водонепроницаемыми (водоупорными) слоями грунта. Такая фильтрация называется напорной (рис. 4.8.1).
 |
| Рис. 4.8.1. Напорная фильтрация. |
• Если водоупорный слой ограничивает поток только снизу, то такая фильтрация называется безнапорной (рис. 4.8.2). Поверхность безнапорного фильтрационного потока называется депрессивной, а кривая свободной поверхности – кривой депрессии. В зависимости от расхода депрессивная поверхность занимает разные положения.
 |
| Рис. 4.8.2. Безнапорная фильтрация. |
• Безнапорное движение грунтовых вод чаще является неравномерным, поскольку гидравлический уклон J, как правило, не равняется уклону водоупорного слоя i (см. рис. 4.8.2).
• Отношение расхода Q ко всей площади фильтрационного потока ω называется скоростью фильтрации:
• В мелкозернистых грунтах (пески, глина, суглинки и т.п.) происходит ламинарная фильтрация, которая характеризуется потерями напора, прямо пропорциональными скорости фильтрации в первой степени.
• В крупнозернистых песках и материалах (гравий, галька, щебень, камень) происходит турбулентная фильтрация, при которой потери напора пропорциональны скорости в степени выше, чем первой.
• При фильтрации вода проходит через поры между частичками грунта. Отношение площади пор в сечении фильтрационного потока ωp ко всей площади сечения ω называется коэффициентом пористости грунта: p = ωp/ω. Его значение обычно находится в пределах p = 0,3…0,5.
• Основной закон фильтрации:
где k – коэффициент фильтрации (см. табл. 4.8.1), зависящий от рода грунта и температуры воды; J – гидравлический уклон, который является потерей напора на единице длины фильтрационного потока:
m – показатель степени, для ламинарной фильтрации m = 1, для турбулентной – m = 0,5…1.
Таблица 4.8.1. Коэффициент фильтрации.
| Грунты | k, см/с |
| Глина Суглинок Супесь Песок: мелкозернистый среднезернистый крупнозернистый Галька и гравий | 1·10 -7 1·10 -7 …1·10 -5 1·10 -5 …1·10 -3 1·10 -4 …1·10 -3 1·10 -3 …1·10 -2 1·10 -2 …1·10 -1 1·10 -1 …1·10 |
• С учетом (6.2) скорость фильтрации
• При ламинарной фильтрации скорости фильтрации малы (V
1 мм/с). В расчетах скоростным напором αV 2 /(2g) пренебрегают и считают, что полный напор равняется пьезометрическому (H0 = H), а гидравлический уклон пьезометрическому (J = ip).
• Прибор Дарси (рис. 4.8.3) представляет собой цилиндр с дырчатым дном и выведенными из боковой поверхности цилиндра пьезометрами. Цилиндр заполняют исследуемым грунтом. Установившееся движение воды через прибор обеспечивается поддержанием постоянной отметки поверхности воды в приборе благодаря сбросу излишка воды в сбросную трубу. Коэффициент ламинарной фильтрации
, (4.8.5)
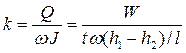
где W – объем воды, проходящей через прибор за время t, 
– площадь сечения цилиндра.
 |
| Рис. 4.8.3. Прибор Дарси для определения коэффициента фильтрации. |
• Равномерное безнапорное движение грунтовых вод. Гидравлический и пьезометрический уклоны равны уклону водоупорного слоя i (рис. 4.8.4):
 |
| Рис. 4.8.4. Равномерное безнапорное движение грунтовых вод. |
глубина равномерного движения
, (4.8.8)
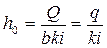
где ω = bh0 – площадь сечения потока, q = Q/b – расход на единицу ширины потока.
• Неравномерное безнапорное движение грунтовых вод. В этом случае (рис. 4.8.5) уклон кривой депрессии
, (4.8.9)
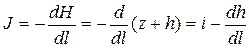
где H – пьезометрический напор над плоскостью сравнения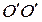 
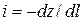
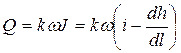
, z – отметка водоупорного слоя, h – глубина фильтрационного потока, 
– уклон водоупорного слоя. Тогда расход
. (4.8.10)
 |
| Рис. 4.8.5. Неравномерное безнапорное движение грунтовых вод. |
Расход на единицу ширины потока (удельный расход)
. (4.8.11)
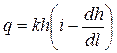
Получено дифференциальное уравнение неравномерного плавноизменяющегося движения грунтовых вод.
• Интегрируя дифференциальное уравнение (4.8.11), получаем расстояние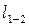 
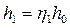
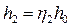
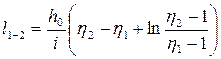
между сечениями с глубинами 
и 
:
. (4.8.12)
• На практике часто бывает, что уклон водоупорного слоя i = 0. Тогда уравнение (4.8.11) приобретает вид:
. (4.8.13)
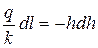
Интегрированием уравнения (4.8.13) получаем уравнение Дюпюи:
. (4.8.14)
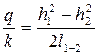
• Дренаж – это система подземных каналов (дрен), через которые осуществляется осушение сельскохозяйственных земель, отвод от сооружений грунтовых вод и снижение их уровня. Воду из дренажной сети выводят за границы осушаемой территории.
• Приток воды к галерее, расположенной на водоупорном слое (рис. 4.8.6). Согласно уравнению Дюпюи (4.8.14), удельный приток воды с одной стороны дренажной галереи (рис. 4.8.6)
, (4.8.15)
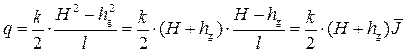
где q – удельный приток с одной стороны галереи, l – длина влияния галереи (расстояние от галереи, на котором уровень грунтовых вод практически не снижается), H – толщина водоносного слоя,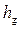 
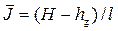
– глубина воды в галерее, 
– средний уклон кривой депрессии, значение которого в зависимости от вида грунта приведены в табл. 4.8.2.
 |
| Рис. 4.8.6. Галерея на водоупорном слое. |
Таблица 4.8.2. Средний уклон кривой депрессии.
| Вид грунта |  |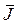
| Плотные глины Глинистые грунты Песчано-глинистые грунты Песок Крупный песок, галька | 0,15 0,1 0,05…0,1 0,005…0,015 0,003…0,005 |
• Подставляя найденное значение q в уравнение Дюпюи
, (4.8.16)
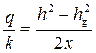
находят глубину воды h на расстоянии x от галереи и строят кривую депрессии.
• Приток воды к галерее, размещенной выше водоупорного слоя (рис. 4.8.7). Такая галерея называется висячей. Удельный приток
где удельный приток через одну боковую стенку
. (4.8.18)
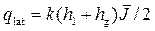
Чтобы найти удельный приток qbot через половину ширины дна, вычисляем значения коэффициентов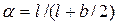 
, 
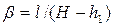
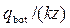
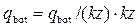
. Потом из графика рис. 4.8.8 находим относительную величину 
и, в конце концов, вычисляем 
. Кривую депрессии можно построить по уравнению (4.8.16) с учетом того, что в этом случае q = qlat.
 |
| Рис. 4.8.7. Висячая галерея. |
 |
| Рис. 4.8.8. График для расчёта притока к висячей галерее. |
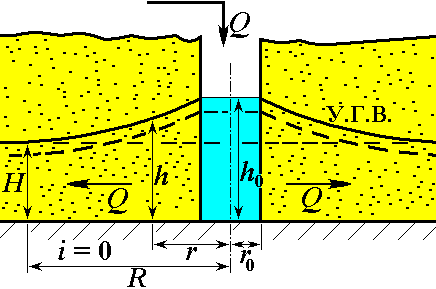
• Приток воды к круглому совершенному дренажному колодцу. Совершенным называется колодец, расположенный на водоупорном слое (рис. 4.8.9). При откачивании воды из колодца глубина в нем будет уменьшаться, но из-за разности уровней грунтовых вод и отметки воды в колодце вода со всех сторон будет притекать к нему по радиальным направлениям. Основной закон фильтрации (4.8.2) принимает вид:
. (4.8.19)
Отсюда дифференциальное уравнение кривой свободной поверхности:
. (4.8.20)
Интегрируя это уравнение, получаем уравнение кривой депрессии для совершенного колодца:
. (4.8.21)
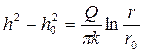
Приток воды к колодцу или необходимая величина откачки
, (4.8.22)
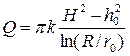
где H – толщина водоносного слоя. Радиус влияния колодца R определяют по эмпирической формуле Зихарда: 
, где глубина откачки 
, [R] = м, k – коэффициент фильтрации, м/с.
 |
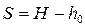
| Рис. 4.8.9. Круглый совершенный дренажный колодец. |
Пример 4.8.1. Определить дебит совершенного дренажного колодца, если отметка статического уровня грунтовых вод H = 15 м, отметка уровня воды в колодце h0 = 10 м, отметка водоупорного слоя 0,00 м, диаметр колодца d = 40 см, радиус влияния колодца R = 150 м, коэффициент фильтрации k = 0,03 см/с.
Решение. Радиус колодца r0 = d/2 = 0,2 м. Дебит совершенного дренажного колодца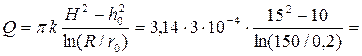 
0,0177 м 3 /с.
• Приток воды к совершенному артезианскому колодцу. Артезианский колодец забирает воду из водоносного слоя, ограниченного сверху и снизу водоупорными грунтами (рис. 4.8.10). Вода в таком слое находится под давлением и называется артезианской. В этом случае статический напор (за пределами радиуса влияния колодца) и напор в любом сечении h отличаются от толщины водоносного слоя a. Дебит колодца
, (4.8.23)
. (4.8.24)
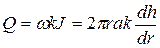
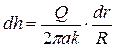
Интегрируя полученное дифференциальное уравнение, имеем:
. (4.825)
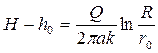
Отсюда дебит артезианского колодца
, (4.8.26)
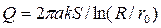
где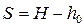 
– глубина откачки.
 |
| Рис. 4.8.10. Совершенный артезианский круглый колодец. |
Пример 4.8.2. Найти дебит совершенного артезианского колодца диаметром d = 25 см, забирающего воду из водоносного песчаного слоя толщиной a = 8 м, если коэффициент фильтрации k = 0,002 см/с, напор в водоносном слое в естественном состоянии H = 20 м, глубина воды в колодце h0 = 10 м.
Решение. Радиус колодца r0 = d/2 = 0,125 м,
глубина откачки 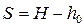= 10 м,
радиус влияния колодца 
134,2 м,
0,00144 м 3 /с.
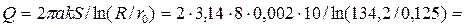
• Совершенный поглощающий круглый колодец. Такой колодец служит для сброса поверхностной воды, которая фильтруется в водоносный слой (рис. 4.8.11). Кривая депрессии в этом случае имеет форму, обратную к кривой депрессии дренажного колодца (рис. 4.8.9). Поглощающая способность поглощающего колодца
. (4.8.27)
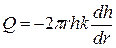
Эта формула отличается от (4.8.19) только знаком “–”, который показывает, что в этом случае вода движется от колодца, а не к нему. После интегрирования получим:
. (4.8.28)
 |
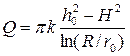
| Рис. 4.8.11. Совершенный поглощающий круглый колодец. |
• Фильтрация воды через земляные плотины.
На рис 4.8.12 показана Асуанская земляная плотина.
 |
| Рис. 4.8.12. Асуанская земляная плотина. Египет. |
• Рассмотрим однородную (из однородного грунта, т.е. с постоянным коэффициентом фильтрации k) земляную плотину на водоупорном основании (рис. 4.8.13). Сила давления воды в водохранилище направлена по нормали к верховому откосу плотины, поэтому фильтрационный поток входит в тело плотины под прямым углом, а потом его линии течения на участке AB приобретают вогнутый характер. На дальнейшем пути BC кривая депрессии имеет форму, подобную кривой притока к дренажной галерее (см. рис. 4.8.6). После точки C часть фильтрационного потока выходит за промежуток высачивания CD, а часть – на затопленный откос DE. Расчет фильтрации основывается на разделении фильтрационного потока на три клина.
 |
| Рис. 4.8.13. Однородная плотина на водоупорном основании. |
• Верховой клин ограничен верховым откосом плотины и вертикальной плоскостью, проходящей через точку B, размещенную на одной вертикали с бровкой плотины. Для верхового клина
, (4.8.29)
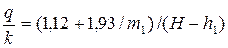
где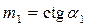 
– коэффициент заложения верхового откоса, H и h1 – напоры в начале и в конце верхового клина.
• Средний клин соответствует участку BC, движение на котором описывается уравнением Дюпюи:
, (4.8.30)
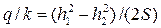
где S – длина среднего клина, т.е. расстояние между живыми сечениями фильтрационного потока, проведенными через точки B и C:
, (4.8.31)
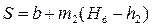
где b – ширина плотины по верху, Hd – высота плотины, 
– коэффициент заложения откоса низовой грани, h2 – глубина в сечении, проходящем через точку C.
• Низовой клин соответствует участку CE. Для низового клина
. (4.8.32)
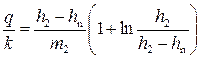
• Через все три клина проходит один и тот же расход q, поэтому решая задачу о фильтрации через плотину, имеем четыре неизвестных величины: q, h1, h2, S, которые можно определить, решив систему из четырех уравнений: (4.8.29), (4.8.30), (4.8.31), (4.8.32).
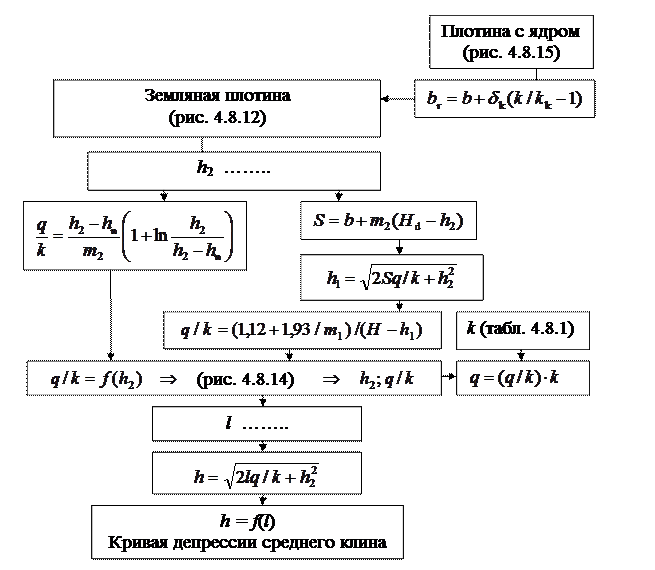
Пример 4.8.3. Определить фильтрационный расход на 1 м длины плотины и построить кривую депрессии при отсутствии воды в нижнем бьефе (hn = 0), если Hd = 14 м, H = 12 м, b = 10 м, m1 = 3, m2 = 2, k = 0,4 м/сут (рис. 4.8.14).
 |
| Рис. 4.8.14. Однородная плотина на водоупорном основании при отсутствии воды в нижнем бьефе. |
Решение. Используем систему уравнений (4.8.29), (4.8.30), (4.8.31), (4.8.32) при hn = 0 и известных Hd, H, b, m, m2. Тогда получим:
;
;
;
.
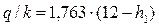
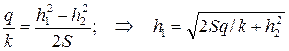
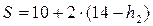
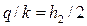
Назначаем несколько значений h2 и выполняем расчеты, результаты которых заносим в табл. 4.8.3. По результатам расчетов строим линии а и б зависимости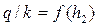 
(рис. 4.8.15).
Таблица 4.8.3. Расчёт параметров фильтрации через плотину.
| h2, м | 3,0 | 3,5 | 4,0 |
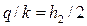| , м; линия а на рис. 4.8.14 | 1,50 | 1,75 | 2,00 |
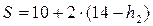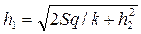| , м | |||
 , м | 10,25 | 10,99 | 11,66 |
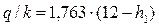| , м; линия б на рис. 4.8.14 | 3,09 | 1,78 | 0,60 |
 |
| Рис. 4.8.15. Графическое определение параметров фильтрации через плотину. |
Из графика рис. 4.8.15 получаем:
Тогда q = (q/k)·k = 1,76∙0,4 = 0,704 м 2 /сут.
Расстояние 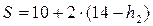= 30,94 м.
Кривую депрессии на участке среднего клина (рис. 4.8.14) строим согласно уравнению (4.8.30) для значений l = 0…S. Результаты расчетов приведены в табл. 4.8.4.
Таблица 4.8.4. Расчёт кривой депрессии.
| l, м | 30,94 | ||||||
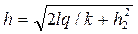 , м | 3,53 | 5,48 | 6,90 | 8,01 | 9,10 | 10,02 | 11,02 |
• Фильтрация через земляную плотину с ядром. Для уменьшения фильтрации через земляную плотину, в ней устраивается ядро из малопроницаемого грунта, например, глины (рис. 4.8.16а). Фильтрационный поток в ядре заменяют эквивалентным потоком в прямоугольном массиве грунта, из которого изготовлена плотина, шириной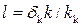 
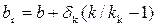
, где k и kk – коэффициенты фильтрации грунта соответственно тела плотины и ядра, δk – средняя толщина ядра. Итак, расчет фильтрации через земляную плотину с ядром сводится к расчету плотины из однородного грунта с теми же коэффициентами заложения откосов, но с большей шириной по верху, которая называется приведенной (рис. 4.8.16б):
. (4.8.33)
 |
| Рис. 4.8.16. Земляная плотина с ядром и приведенная плотина. |
Рис. 4.8.17. Схема к расчёту фильтрации.
Рис. 4.8.18. Схема к расчёту фильтрации сквозь земляную плотину.
Источник